Hablar de las Lectures on Physics de Feynman y no quedarse corto en halagos es todo un reto.
Se las debemos al trabajo de muchas personas, no
solo al de Feynman. Pero es única y exclusivamente de Feynman su contenido, que
preparó con gran ahínco, intentando que los jóvenes estudiantes que tomaran sus
primeros cursos en física universitaria saborearan todo lo que esta ciencia
tiene que ofrecer.
Aunque si nos retrotraemos aún más en el tiempo, a
quien debemos estos libros no es a
Feynman, sino a su padre, Arthur Melville Feynman.
Pese a que Arthur era un humilde gerente de ventas,
era un apasionado de la ciencia, y esa pasión se contagió a su hijo, Richard.
Aprovechaba todas las ocasiones que el día a día le presentaba para plantear
cuestiones al pequeño Dick1, con un enfoque que hoy día diríamos que
favorece el aprendizaje significativo (aquel que perdura, pues
apoya sus bases sobre lo ya aprendido).
Por ejemplo, Arthur leía a su hijo de pequeño la Enciclopedia Británica. Richard relata
cómo, cuando llegaban a la entrada sobre el Tyrannosaurus
Rex y leían que su tamaño era de siete metros y medio, su padre detenía la
lectura e incitaba al joven Richard a que imaginase en ese momento al Tyrannosaurus. Dado su tamaño, le decía, su cabeza asomaría por nuestra ventana ahora mismo.
Pero, y seguía leyendo la entrada de la enciclopedia, aquí dice que su cabeza es un metro ochenta de
ancha, por lo que ¡no entraría por el hueco de nuestra ventana!
A esto me refiero con que el aprendizaje planteado
por el padre era significativo. Leer la descripción del Tyrannosaurus no lleva a nada. Plantearse, en cambio, cómo se vería
al lado de nuestra casa, cuyas medidas tenemos interiorizadas, seguramente sí
perdure en la memoria.
Esta manera de aprender sobre el mundo fue calando
en el pequeño Richard. Otra anécdota interesante al respecto viene de cuando,
juntándose con sus amigos y hablando de lo que habían aprendido sobre pájaros
en excursiones con sus padres, uno le preguntó a Feynman: ¿Qué pájaro es aquel de allí?, a lo que nuestro protagonista no supo qué responder. Su amigo le dijo
que era un tordo petimarrón, y que su padre no le estaba enseñando nada en sus
excursiones.
Feynman discrepaba.
En sus excursiones, cuando su padre le decía ¿Ves aquel pájaro?, seguidamente
inventaba toda clase de nombres para este, uno por cada idioma, y le dejaba
claro que podría saber el nombre del pájaro en todos los idiomas del mundo y
aun así no saber nada sobre él. Le proponía seguidamente, pues, observar el pájaro y ver qué está haciendo. Eso es
lo que debería importar.
Veían, por ejemplo, que los pájaros se picoteaban
las plumas. Arthur le preguntaba a su hijo entonces: ¿Por qué piensas que hacen eso? Richard proponía una hipótesis y su padre, en lugar de desecharla
directamente por errónea (conocedor de la verdadera razón), le incitaba a
comprobarla in situ. Si Richard le
decía: quizá se ajustan las
plumas, pues a lo mejor al volar se las desordenan, el padre le proponía que se fijaran si dicha conducta se daba más en
los pájaros que se acababan de posar de su vuelo (y comprobaban que no era esa
la razón).
Es decir, Arthur no quería que su hijo memorizase
datos, quería que adquiriera la capacidad de plantearse hipótesis sobre el
mundo y comprobarlas. Que dudara de todo y de todos, y construyera su propio
conocimiento. Que adquiriera la mente que creía que un científico debía tener.
Siendo Feynman ya adulto, tuvo oportunidad de
tomarse unos años sabáticos en Brasil (donde adquiriría su famoso gusto por la
percusión) e impartir clase a estudiantes de física. Y allí notó algo que ya
había visto muchas veces antes: que el conocimiento de los demás era muy frágil. Los estudiantes
memorizaban, pero no conectaban cada nuevo concepto con algo anterior en su
memoria entendiendo cómo de uno se derivaba el otro. Y eso les impedía razonar.
Cuando Feynman murió, en la pizarra de su despacho
(Figura 1) quedó escrita una frase que no solo había guiado toda su
investigación, sino también su manera de enseñar:
Fig.1 Esquina superior izquierda de la pizarra en el despacho de Feynman.
«What I cannot
create, I do not understand», que recuerda al viejo proverbio chino
atribuido a Confucio: «Oigo y olvido, veo
y recuerdo, hago y aprendo». Y a esto nos animaba Feynman. A ser los dueños
de nuestro aprendizaje. Por eso, tras la frase anterior, leemos: «Know how to solve every problem that has been solved».
Y con esto en mente, Feynman encaró la preparación
de sus Lectures bajo petición de
Matthew Sands, que habrían de empezar en septiembre de 1961.
Yo llegué a ellas de manera fortuita.
Cuando el curso antes a entrar en la universidad la
idea de estudiar física rondaba mi cabeza, saqué un libro de la biblioteca de
mi ciudad titulado Electrodinámica
cuántica. La extraña teoría de la luz y la materia2, únicamente
guiado por su rimbombante nombre. Ya había leído otros libros de divulgación
anteriormente, como Breve historia del
tiempo o El universo elegante.
Esto no se sentía igual.
Feynman no tenía otro modo de hacer las cosas. En la
divulgación mainstream, el escritor
(usualmente científico) renuncia a tratar de que interiorices los conceptos.
Solo quiere darte a probar la miel y dejarte desarrollar el gusto por ella.
Pues los que hemos visto las matemáticas detrás de cualquier teoría física
coincidimos con Euclides: No hay camino
real hacia la geometría.
Feynman compartía dicha opinión. Pero le daba
vueltas y vueltas a todo lo que quería explicar y acababa encontrando una manera
de que, en su versión divulgativa, lo que te estaba contando fuera lo más
cercano posible al trasfondo matemático real del problema en cuestión.
Así, en dicho libro, consigue que entiendas los
fenómenos de la propagación de la luz y su interacción con la materia en base a
unas reglas sencillas y muchos dibujos (que tienen detrás a sus niñas bonitas:
las integrales de camino y los diagramas de Feynman).
Con su nombre ya en mente, un día vi en la
biblioteca de mi instituto tres volúmenes azules en paralelo. En el lomo se
leía en cursiva y con una bonita tipografía «Feynman», seguido de la palabra FÍSICA
en grande.
Tras ojear su índice, las pedí prestado sin dudarlo
y leí los primeros capítulos de su primer volumen. Aquello era otra manera de
mostrar la física, muy alejada al escueto libro de texto al que estaba
habituado. Si quedaba alguna duda sobre si estudiar física, se disipó.
En la universidad tuve la oportunidad de sacarlas
siempre que quise de la biblioteca. Cuando estudiábamos cierto tema en alguna
asignatura, yo trataba de ver si había sido desarrollado en alguna lección y
leerlo por mi cuenta. Feynman siempre encontraba otra manera de contártelo.
Desde la conservación del momento (lección 10, Vol. I), vista casi en los
primeros días de la carrera (pasando por encima, centrándonos directamente en
su aplicación) a la propagación de electrones en redes cristalinas que fue el
tema de mi Trabajo de Fin de Grado. Las Lectures
tenían una lección para casi todo.
Pasaron los años y en cuanto pude las adquirí de
segunda mano en la misma edición que las tenía la biblioteca de mi instituto. Y
pasó algo más de tiempo y me convertí en profesor de Física y Química en
secundaria y Bachillerato.
Revisitar las Lectures
para preparar mis clases es algo que hago de manera automática, casi sin
reflexionarlo.
Hoy en día los alumnos pueden llegar a 4º de ESO
(15-16 años) y aun no manejar con soltura las funciones (menos aun entender qué
es una derivada). Los alumnos que comenzaban aquel curso de 1961 tampoco tenían
por qué (muchos continuarían sus estudios en otras ciencias, como medicina o
geología). Así que Feynman construye el concepto de derivada poco a poco a
partir del concepto de velocidad instantánea (lección 8, Vol. I). Con esa
manera de enfocar el asunto los chicos y chicas de 16 años a los que me suelo
enfrentar lo entienden enseguida.
En segundo de Bachillerato (17-18 años) los alumnos
saben derivar (con un poco de suerte, dependiendo de lo bien que haya ido en
matemáticas el curso anterior). Pero ni mucho menos saben integrar ni qué es
una ecuación diferencial. Que la fuerza gravitatoria haga que los planetas se
muevan en elipses en lugar de circunferencias3 cuando es una fuerza
que solo depende de la distancia es algo chocante (que resolviendo una ecuación
diferencial sencilla sale directo). De nuevo, Feynman piensa: ¿de qué manera
transmitir tan bello hecho a alumnos que no tienen las herramientas matemáticas
necesarias? Y se saca de la manga la mejor respuesta posible: la resolveremos
numéricamente (capítulo 9, Vol. I).
Es algo fácil de entender: discretizamos el problema
en pasos finitos de tiempo y calculamos la posición y la velocidad en un paso
dado basándonos en los valores del paso anterior.
Fig.2 ¡Los alumnos pueden ver cómo la gravedad produce órbitas elípticas ellos mismos con una hoja de cálculo!
No solo para los cursos «altos» es que las Lectures se muestran útiles. A los
alumnos de segundo de ESO (13-14 años) hay que hablarles del concepto más
abstracto de toda la física: la energía (y su conservación). De nuevo, Feynman
viene al rescate y nos regala una deliciosa analogía al comienzo del capítulo 4
del primer volumen con un niño que juega con sus bloques y cuyo número ha de
conservarse.
Pero si hay una lección que siempre me ha alucinado
y que creo que se conoce poco4 es la 42 del segundo volumen, en la
que Feynman nos enseña una manera sencilla de entender por qué la gravedad
curva el espaciotiempo sin recurrir a analogías ya muy gastadas en la
divulgación de mallas elásticas que se deforman.
Veamos cómo lo hace.
Imagina a un hombre en un cohete en el espacio
vacío, alejado de toda influencia, desconocedor de su situación. Supón que el
cohete está acelerando uniformemente en cierta dirección. En tal caso, el
hombre permanecerá pegado al suelo, igual que tú te pegas al asiento de tu
coche cuando este acelera. Si ahora dejara caer un objeto de su mano, este
caería al suelo aceleradamente, de la
misma manera que caen los objetos en la superficie terrestre.
La pregunta surge sola: ¿cómo puede discernir el
hombre del interior si está en un cohete en el espacio vacío acelerando o parado sobre la superficie de la Tierra, sujeto a su gravedad?
Y la respuesta es simple: no puede.
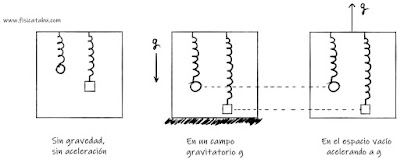
Fig.3 El alargamiento de un muelle es igual cuando el sistema sufre una aceleración uniforme que cuando se deja en un campo gravitatorio de igual magnitud.
Y a tal hecho se le llama principio de equivalencia (débil en este caso): no podemos
distinguir un campo gravitatorio uniforme de una aceleración constante por
ningún experimento (de hecho, ¡se miden en las mismas unidades!).
Resulta que tan sencillo principio tiene profundos
impactos. Por ejemplo, podemos razonar a partir de este que la luz se curva. Si
dentro de nuestro cohete lanzáramos un haz de luz, dado que el cohete acelera,
veríamos algo similar a las imágenes de la figura 4.
Si ahora juntamos todas las imágenes, nos queda:
Fig.4 La evolución de un haz de luz debe ser igual cuando el sistema sufre una aceleración uniforme que cuando se deja en un campo gravitatorio de igual magnitud.
Claro, si cualquier experimento ha de ocurrir igual
en un sistema que acelera que en uno sujeto a un campo gravitatorio… ¡la luz ha
de curvarse en campos gravitatorios!
Y no solo eso: el tiempo se dilata en campos gravitatorios.
Imaginemos ahora un cohete con dos relojes, uno en
su base y otro en su parte más alta. Cada segundo (de su reloj) el superior
emite un pulso láser al inferior. Si nuestro cohete está en el espacio vacío,
podemos sincronizar los relojes y la recepción del pulso tendrá lugar segundo a
segundo medido por el reloj inferior también.
Ahora bien, ¿y si nuestro cohete comienza a
acelerar?
Dado que el cohete acelera, el pulso no tiene que
recorrer toda la longitud del cohete, pues el reloj inferior lo encuentra
«antes» de lo que lo haría si no acelerase. Si el primer pulso recorre una
longitud
Fig.5 Cohete acelerando con dos relojes.
Por tanto, si un observador observa el reloj
inferior debe concluir que el reloj superior avanza más deprisa (mientras que
un observador observando el superior concluiría que el reloj inferior va más
lento).
De nuevo, si los experimentos en una nave con
aceleración constante son indistinguibles que los realizados en un campo
gravitatorio… ¡el tiempo se dilata en campos gravitatorios!
Concretamente, va más rápido a mayor altura sobre la
superficie (cuanto más alejados estemos de la influencia gravitatoria). Una
consecuencia palpable de esto es que el reloj interno de los satélites GPS ha
de ajustarse para tener este efecto en cuenta y estar sincronizado con la
Tierra (de no hacerlo acarrearía un error de 11 km por cada día sin
sincronizarse).
Y ya, al fin, vayamos a la gran idea planteada por
Feynman en esta lección: ¿cómo usamos estas consecuencias del principio de
equivalencia para entender que nuestro espaciotiempo es curvo?
Primero tenemos que entender qué es un espacio
curvo. Y como todo en matemáticas, debemos hacerlo recurriendo a definiciones
operativas. Aunque para poder visualizarlas, bajemos a dos dimensiones
espaciales. Imaginemos que somos una pequeña hormiga en una superficie plana.
Sin duda, en dicha superficie construcciones como las siguientes funcionan a la
perfección:
- Para trazar un cuadrado, se parte de un punto, se avanza cierta
cantidad, se giran noventa grados, y se repite tres veces (girando siempre en
el mismo sentido), llegando al mismo punto.
- Habiendo trazado un triángulo, si se suman sus ángulos internos
obtendremos 180 grados.
- Habiendo trazado un círculo (lugar geométrico de todos los puntos que
están a la misma distancia de uno dado), la división de su longitud entre su
diámetro da 3,14159…. (
Ahora, traslademos a la hormiga a una esfera (como
un balón de baloncesto). Dada su pequeñez, la hormiga no puede saber que se
encuentra en una esfera (igual que nosotros no vemos la «esfericidad» de
nuestro planeta). Pero puede repetir dichas construcciones, a ver qué ocurre.
Fig.6 Las “dificultades” de nuestra hormiga.
Sobre una esfera, nuestro procedimiento para hacer
un cuadrado no conseguiría que la hormiga acabara en el punto de partida, los
ángulos de cualquier triángulo sumarían más de 180 grados y en cualquier
círculo el cociente entre su longitud y su diámetro no daría 3,14159…
Nuestra tridimensionalidad nos permite ver qué está
ocurriendo, pero la hormiga no tiene esa opción. De hecho, se puede estudiar la
curvatura de un espacio en matemáticas sin necesidad de embeberlo en un espacio
de mayor dimensión. Y eso es lo que hacemos nosotros al estudiar nuestro
universo.
Para justificar, pues, que nuestro espaciotiempo sea
curvo podemos recurrir a una artimaña similar: tratar de trazar un cuadrado,
mas esta vez en el propio espaciotiempo.
En aras de poder visualizarlo, reduzcamos aún más
las dimensiones a una espacial y una temporal. Sea la altura respecto al suelo
(en un mundo con gravedad) el eje vertical y el tiempo medido por nuestro reloj
el eje horizontal5.
Si, quietos a cierta altura, dejamos transcurrir
cien segundos, se trazará un segmento horizontal en nuestro diagrama. Subamos
ahora a cien metros de altura y repitamos el experimento: dejamos correr
nuestro reloj cien segundos medidos a
dicha altura. El segmento ahora trazado es más corto que el anterior, como
hemos demostrado ya por el principio de equivalencia, por lo que no nos es
posible cerrar nuestra figura si desde el punto inferior trazamos una línea
vertical.
Fig.7 Secuencia del intento de trazar un cuadrado en el “espaciotiempo” de dos dimensiones, una espacial (vertical) y una temporal (horizontal).
Como vemos, el principio de equivalencia implica que
el espaciotiempo se curve en presencia de gravedad. No por nada lo calificó
Albert Einstein como la idea más feliz de
su vida.
¿Se entiende ya a lo que me refería con la manera de
enfocar los temas de Feynman? En un curso a universitarios cualquier otro
habría tirado por otro camino. Feynman no. Tras muchas vueltas se le ocurre una
manera de que en un par de horas entiendas cómo el principio de equivalencia,
base de la relatividad general, implica que el espaciotiempo sea curvo.
Y pese a toda esta genialidad, a Feynman nunca le
terminaron de convencer sus Lectures.
Las veía como un experimento, una manera de presentar la física a estudiantes
que comenzaban en la universidad que nunca antes se había llevado a cabo. Y
creía que su experimento había fallado, vistos los resultados que los alumnos
obtenían en los exámenes.
Y en parte puedo estar de acuerdo con Feynman. Es
francamente difícil que las Lectures
por sí solas te ayuden a enfrentar los problemas habituales que se te
presentarán en física. Pero creo que pensar que ese es su cometido es un error.
Las Lectures
On Physics son la mejor compañía para aquel que ya sabe algo de física.
Para el estudiante con motivación, que amplía lo visto. Para el profesor que
busca maneras distintas de enfocar un tema, y su experiencia le sabrá decir
cómo aprovecharlas para volver sus clases más pedagógicas.
Y, aunque Feynman creía que no sirvieron, o que quizá
sus clases no gustaron, sin duda se equivocaba. El físico Kip Thorne (profesor
emérito de la cátedra «Profesor Feynman» del Caltech) encuestó a estudiantes
que asistieron a las lecciones de Feynman recogiendo opiniones tales como «Era
como ir a la iglesia», «Las Lectures
fueron probablemente lo más importante que obtuve de Caltech» o «Recuerdo y aun
puedo sentir la alegría de Feynman por el descubrimiento».
Pese a todo, Feynman era el más positivo de los
positivos. Y por eso, aunque no estuviera convencido del resultado, finalizó
así el prefacio a las Lectures:
Pienso, sin embargo, que
la solución a este problema educativo [refiriéndose a no dejar a ningún
estudiante atrasado] no es otra que darse cuenta que la enseñanza solo puede
realizarse cuando hay una relación individual directa entre un estudiante y un
buen profesor, situación en la cual el estudiante discute las ideas, piensa en
las cosas y habla sobre ellas. Es imposible aprender simplemente asistiendo a
una clase, o simplemente resolviendo los problemas asignados. Pero en los
actuales momentos tenemos tantos estudiantes a quienes enseñar que tenemos que
encontrar un sustituto de lo ideal. Quizás mis lecciones ejerzan alguna
contribución. Quizás en algún lugar pequeño donde sea posible una relación
individual entre profesores y estudiantes, estos obtengan alguna inspiración o
algunos conceptos de estas lecciones. Quizá entonces, también el proceso de
fijar el material sea más alegre y placentero para ellos y dé origen al
desarrollo de algunas ideas.







No hay comentarios:
Publicar un comentario